An Introduction to Pseudo-semi-supervised Learning for Unsupervised Clustering

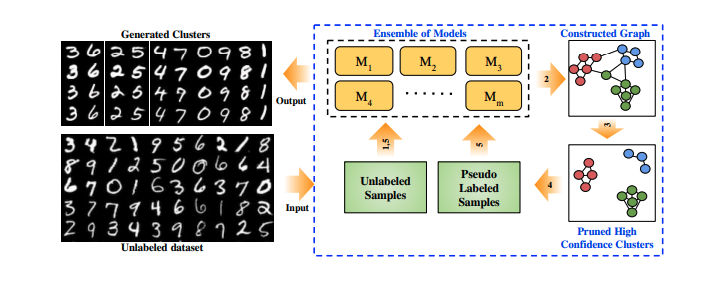
This post gives an overview of our deep learning based technique for performing unsupervised clustering by leveraging semi-supervised models. An unlabeled dataset is taken and a subset of the dataset is labeled using pseudo-labels generated in a completely unsupervised way. The pseudo-labeled dataset combined with the complete unlabeled data is used to train a semi-supervised model.

This work was published in ICLR 2020 and the paper can be found here and the source code can be found here.

Introduction

In the past 5 years, several methods have shown tremendous success in semi-supervised classification. These models work very well when they are given a large amount of unlabeled data along with a small amount of labeled data.

The unlabeled data helps the model to discover new patterns in the dataset and learn high-level information. The labeled data helps the model to classify the data-points using the learned information. For example, Ladder Networks can yield 98% test accuracy with just 100 data-points labeled and the rest unlabeled.

In order to use a semi-supervised classification model for completely unsupervised clustering, we need to somehow generate a small number of labeled samples in a purely unsupervised way. These automatically generated labels are called pseudo-labels.

It is very important to have good quality pseudo-labels used to train the semi-supervised model. The classification performance drops if there is a large amount of noise in the labels. Hence, we are okay with having less number of pseudo-labeled data points, given that the noise in the pseudo-labels is less.

A straightforward way to do this is the following:

1. Start with an unlabeled dataset.
2. Take a subset of the dataset and generate pseudo-labels for it, while ensuring the pseudo-labels are of good quality.
3. Train a semi-supervised model by feeding the complete unlabeled dataset combined with the small pseudo-labeled dataset.

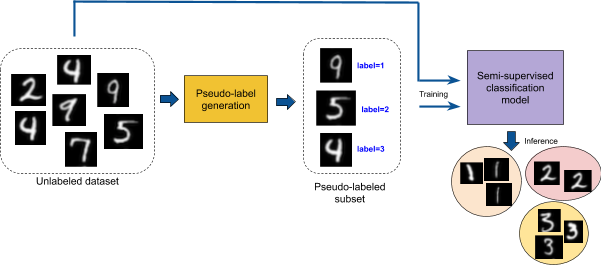
This approach uses some elements of semi-supervised learning but no actual labeled data-points are used. Hence, we call this approach pseudo-semi-supervised learning.

Generating pseudo-labels

Generating high-quality pseudo-labels is the trickiest and the most important step to get good overall clustering performance.

The naive ways to generate a pseudo-labeled dataset are

1. Run a standard clustering model on the entire dataset and make the pseudo-labels equal to the cluster IDs from the model.
2. Run a standard clustering model with way more number of clusters than needed. Then only keep a few clusters to label the corresponding data-points while discarding the rest.
3. Run a standard clustering model and only keep the data-points for which the confidence by the model is more than a certain threshold.

In practice, none of the ways described above work.

The first method is not useful because the pseudo labels are just the clusters returned by the standard clustering model, hence we can’t expect the semi-supervised model to perform better than that.

The second way does not work because there is no good way to select distinct clusters.

The third way does not work because in practice the confidence of a single model is not an indicator of the quality.

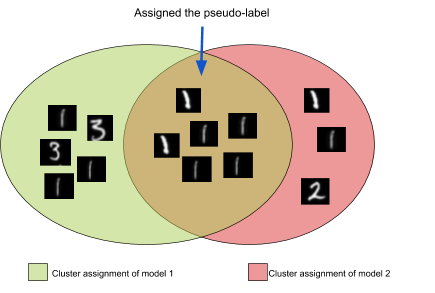
After experimenting with several ways to generate a pseudo-labeled dataset, we observed that consensus of multiple unsupervised clustering models is generally a good indicator of the quality. The clusters of the individual models are not perfect. But if a large number of clustering models assign a subset of a dataset into the same cluster, then there is a good chance that they actually belong to the same class.

In the following illustration, the data points which are in the intersection of the cluster assignments of the two models could be assigned the same pseudo-label with high confidence. Rest can be ignored in the pseudo-labeled subset.

Using a graph to generate the pseudo-labels

There is a more formal way to generate the pseudo-labeled dataset. We first construct a graph of all the data-points modeling the pairwise agreement of the models.

The graph contains two types of edges.

1. Strong positive edge - when a large percentage of the models think that the two data-points should be in the same cluster
2. Strong negative edge - when a large percentage of the models think that the two data-points should be in different clusters.

It is possible that there is neither a strong positive edge nor a strong negative edge between the two data-points. That means that confidence of the cluster assignments of those data points is low.

After constructing the graph, we need to pick K mini-clusters such that data-points within a cluster are connected with strong positive edges and the data-points of different clusters are connected with strong negative edges.

An example of the graph is as follows:

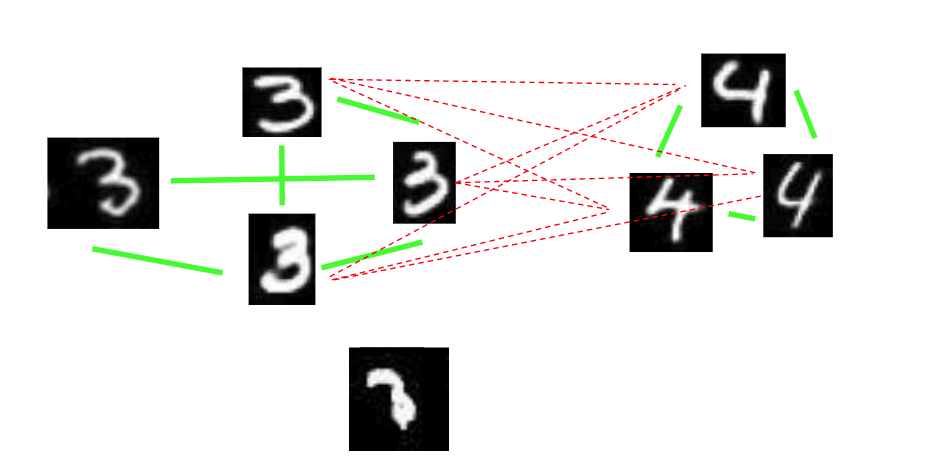Example of a constructed graph. Strong positive edge - green , Strong negative edge - red

We first pick the node with the maximum number of strong positive edges. That node in circled in the example:

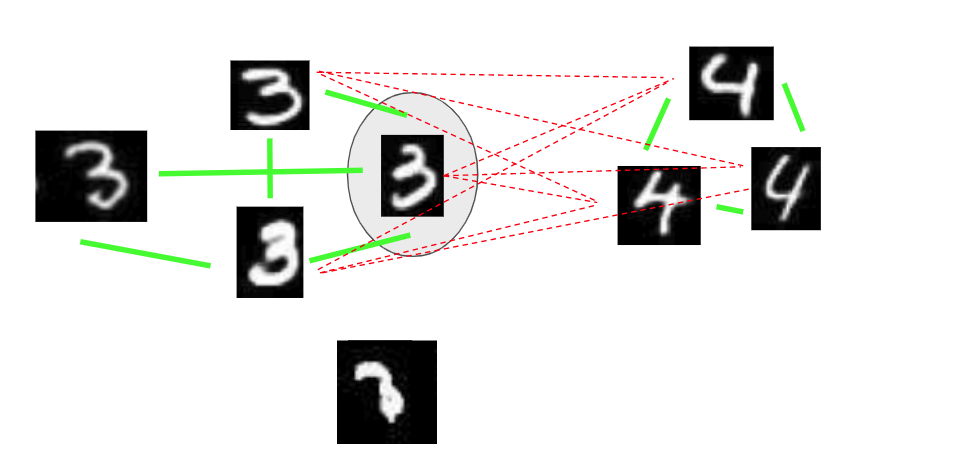The selected node is circled

We then assign a pseudo-label to the neighbors connected to the selected node with strong positive edges:

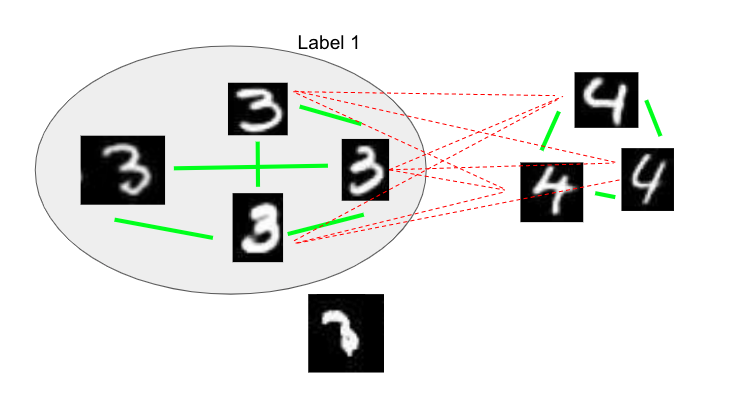
Nodes which are neither connected with a strong positive edge nor a strong negative edge are removed because we can’t assign any label with high confidence:

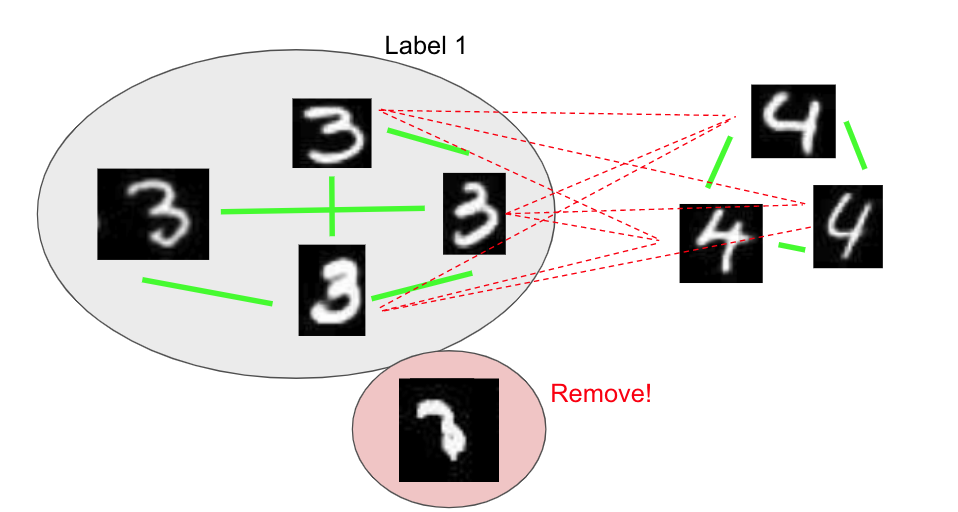
We then repeat the steps K more times to get K mini-clusters. All data-points in one mini-cluster are assigned the same pseudo-label:

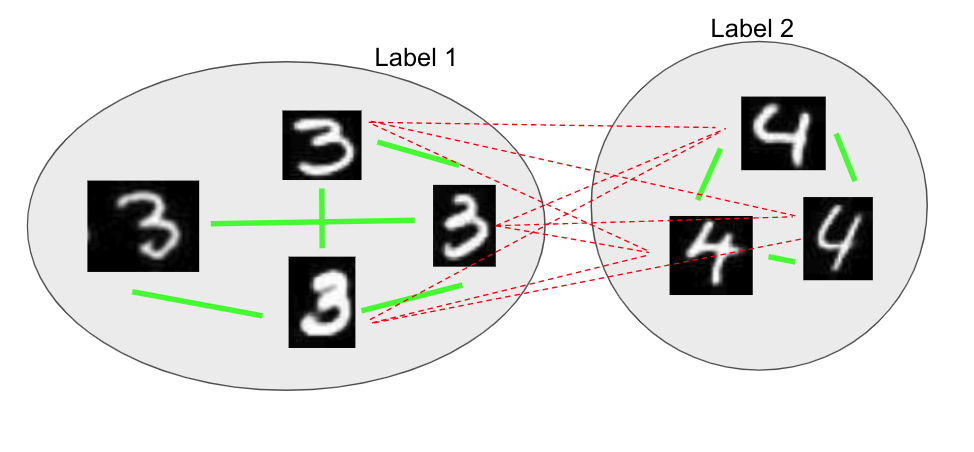The final pseudo-labeled subset

We can see that a lot of data-points will be discarded in this step, hence it’s ideal to send these pseudo-labeled data points to a semi-supervised learning model for the next step.

Using pseudo-labels to train semi-supervised models

Now we have a pruned pseudo-labeled dataset along with the complete unlabeled dataset which is used to train a semi-supervised classification network. The output of the network is a softmaxed vector which can be seen as the cluster assignment.

If the pseudo labels are of good quality, then this multi-stage training yields better clustering performance compared to the individual clustering models.

Rather than having separate clustering and semi-supervised models, we can have a single model that is capable of performing unsupervised clustering and semi-supervised classification. An easy way to do this to have a common neural network architecture and apply both the clustering losses and the semi-supervised classification losses.

We decided to use a semi-supervised ladder network combined with information maximization loss for clustering. You can read more about different deep learning clustering methods here.

Putting everything together

In the first stage, only the clustering loss is applied. After getting the pseudo-labels, both clustering and classification losses are applied to the model.

After the semi-supervised training, we can extract more pseudo-labeled data points using the updated models. This process of generating the pseudo labels and semi-supervised training can be repeated multiple times.

The overall algorithm is as follows:

1. Train multiple independent models using the clustering loss
2. Construct a graph modeling pairwise agreement of the models
3. Generate the pseudo-labeled data using the graph
4. Train each model using unlabeled + pseudo-labeled data by applying both clustering and classification loss
5. Repeat from step 2

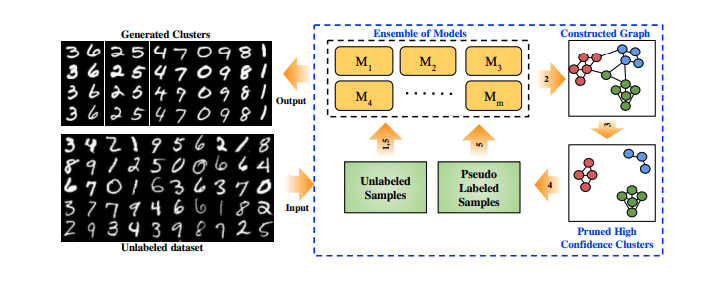Overview of the final system

Playing with the implementation

You can play with the implementation of this system we provided. You need Keras with TensorFlow to run this model.

You can install the package using

pip install git+https://github.com/divamgupta/deep-clustering-kingdra

Load the mnist dataset

import keras
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
x_train = x_train.reshape((-1 , 28*28 ))
x_test = x_test.reshape((-1 , 28*28 ))

Initialize and train the model

from kingdra_cluster.kingdra_cluster import KingdraCluster
model = KingdraCluster( n_iter=5 )
model.fit( x_train )

Get the clustering performance

from kingdra_cluster.unsup_metrics import ACC
preds = model.predict( x_test )
print("Accuracy: " , ACC( y_test  ,  preds ) )

Evaluation

We want our clusters to be close to the ground truth labels. But because the model is trained in a completely unsupervised manner, there is no fixed mapping of the ground truth classes and the clusters. Hence, we first find the one-to-one mapping of ground truth with the model clusters with maximum overlap. Then we can apply standard metrics like accuracy to evaluate the clusters. This is a very standard metric for the quantitative evaluation of clusters.

We can visualize the clusters by randomly sampling images from the final clusters.

Visualizing the clusters of the MNIST dataset. Source : original paper.

Visualizing the clusters of the CIFAR10 dataset. Source : original paper.

Conclusion

In this post, we discussed a deep learning based technique for performing unsupervised clustering by leveraging pseudo-semi-supervised models. This technique outperforms several other deep learning based clustering techniques. If you have any questions or want to suggest any changes feel free to contact me or write a comment below.

Get the full source code from here

References

• Unsupervised Clustering using Pseudo-semi-supervised Learning
• Semi-Supervised Learning with Ladder Networks
• Discriminative Clustering by Regularized Information Maximization